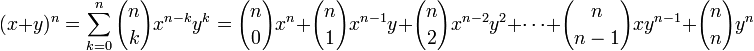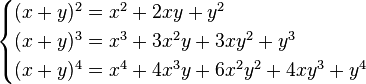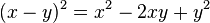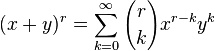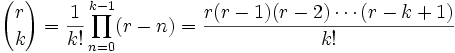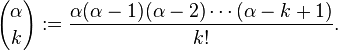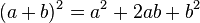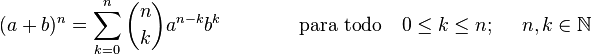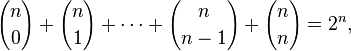Tarea de Analisis combinatorio
Introducción
El análisis combinatorio estudia las distintas formas de agrupar y ordenar los elementos de un conjunto, sin tener en cuenta la naturaleza de estos elementos. Los problemas de arreglos y combinaciones pueden parecer aburridos y quizá se piense que no tienen utilidad pero los teoremas del análisis combinatorio son la base del cálculo de la probabilidad. La probabilidad se encarga de los arreglos y las combinaciones que determinan el número de formas diferentes en que un acontecimiento puede suceder. El análisis combinatorio tiene aplicaciones en el diseño y funcionamiento de la tecnología computacional así como también en las ciencias. La teoría combinatoria se aplica en las áreas en donde tengan relevancia las distintas formas de agrupar elementos.
Técnicas de conteo
A menudo nos encontramos con preguntas del tipo ¿qué proporción de...? ¿Cuál es la probabilidad de...? ¿De cuántas maneras se puede...? Muchas veces, para responder, se necesita un pensamiento sistemático y un poco de información adicional. Hay técnicas y principios matemáticos útiles en situaciones variadas, pero muchas preguntas se pueden responder directamente, contando en forma sistemática, es decir, listando todos los posibles resultados en un orden sistemático, para luego contar cuántos son, o desarrollando reglas de conteo. Algunas soluciones parecen ingeniosas cuando se ven por primera vez (y muchas veces lo son) pero, cuando podemos aplicar nuevamente estos métodos ingeniosos en problemas similares y en situaciones relacionadas entre sí, hemos desarrollado una técnica.
Producto Cartesiano
En teoría de conjuntos, el producto cartesiano de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par del primer conjunto, y el segundo elemento del segundo conjunto.
Por ejemplo, dados los conjuntos A = {1, 2, 3, 4} y B = {a, b}, su producto cartesiano es:
A × B = {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b), (4, a), (4, b)}
El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto.
Un par ordenado es una colección de dos objetos distinguidos como primero y segundo, y se denota como (a, b), donde a es el "primer elemento" y b el "segundo elemento". Dados dos conjuntos A y B, su producto cartesiano es el conjunto de todos los pares ordenados que pueden formarse con estos dos conjuntos:

Puede definirse entonces el cuadrado cartesiano de un conjunto como A2 = A × A.
Ejemplo 1
Sean los conjuntos R = {A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K} y P = {♠, ♥, ♦, ♣} (los rangos y palos de la baraja inglesa). El producto cartesiano de estos conjuntos, B , es el conjunto de todas las parejas rango-palo:
- B = R × P = {(A, ♠), (2, ♠), ..., (K, ♠), (A, ♥), ... (K, ♥), (A, ♦), ..., (K, ♦), (A, ♣), ..., (K, ♣) }
El conjunto B puede entenderse entonces como el conjunto de las 52 cartas de la mencionada baraja.
Ejemplo 2
Sea el conjunto de los números enteros Z = {..., −2, −1, 0, +1, +2, ...}. El producto cartesiano de Z consigo mismo es Z2 = Z × Z = { (0,0), (0, +1), (0, −1), (0, +2), ..., (+1, 0), ... (−1, 0), ... }, es decir, el conjunto de los pares ordenados cuyas componentes son enteros. Para representar los números enteros se utiliza la recta numérica, y para representar el conjunto Z2 se utiliza un plano cartesiano (en la imagen).
Ejemplo 3
Sean los conjuntos T de tubos de pintura, y P de pinceles:

El producto cartesiano de estos dos conjuntos, T × P, contiene todos los posibles emparejamientos de pinceles y tubos de pintura. De manera similar al caso de un plano cartesiano en el ejemplo anterior, este conjunto puede representarse mediante una tabla:

Caso finito
Dado un número finito de conjuntos A1, A2, ..., An, su producto cartesiano se define como el conjunto de n-tuplas cuyo primer elemento está en A1, cuyo segundo elemento está en A2, etc.
|
Puede definirse entonces potencias cartesianas de orden superior a 2, como A3 = A × A × A, etc. Dependiendo de la definición de n-tupla que se adopte, esta generalización puede construirse a partir de la definición básica como:
- A1 × ... × An = A1 × ( A2 × ( ... × An )...)
o construcciones similares.
Caso infinito
En el caso de una familia de conjuntos arbitraria (posiblemente infinita), la manera de definir el producto cartesiano consiste en cambiar el concepto de tupla por otro más cómodo. Si la familia está indexada, una aplicación que recorra el conjunto índice es el objeto que distingue quién es la "entrada k-ésima":
|
donde ∪F denota la unión de todos los Ai. Dado un j ∈ I, la proyección sobre la coordenada j es la aplicación:
En el caso de una familia finita de conjuntos {A1, ..., An} indexada por el conjunto In = {1, ..., n}, según la definición de n-tupla que se adopte, o bien las aplicaciones f : In → ∪i Ai de la definición anterior son precisamente n-tuplas, o existe una identificación natural entre ambos objetos; por lo que la definición anterior puede considerarse como la más general.
Sin embargo, a diferencia del caso finito, la existencia de dichas aplicaciones no está justificada por las hipótesis más básicas de la teoría de conjuntos. Estas aplicaciones son de hecho funciones de elección cuya existencia sólo puede demostrarse en general si se asume el axioma de elección. De hecho, la existencia de funciones de elección (cuando todos los miembros de F son no vacíos) es equivalente a dicho axioma.
Propiedades
El conjunto vacío actúa como el cero del producto cartesiano, pues no posee elementos para construir pares ordenados:
|
El producto cartesiano de dos conjuntos no es conmutativo en general, salvo en casos muy especiales. Lo mismo ocurre con la propiedad asociativa.
|
Puesto que el producto cartesiano puede representarse como una tabla o un plano cartesiano, es fácil ver que el cardinal del conjunto producto es el producto de los cardinales de cada factor:
- El producto cartesiano de un número finito de conjuntos finitos es finito a su vez. En particular, su cardinal es el producto de los cardinales de cada factor:
- El producto cartesiano de una familia de conjuntos no vacíos que incluya algún conjunto infinito es infinito a su vez.
ORDENACIONES
Ordenación simple
Son ordenaciones simples todas las agrupaciones de k elementos, dispuestos linealmente, que se pueden formar a partir de n elementos distintos ( k n ), sin que ninguno se repita. Estas agrupaciones se diferencian entre sí, por los elementos que las componen o por su orden.
El número de variaciones de k elementos que pueden formarse a partir de n elementos distintos ( Vkn ) , es:

Ordenación con repetición
Son ordenaciones con repetición, todas las agrupaciones de k elementos, dispuestos linealmente, que se pueden formar a partir de n elementos distintos, donde cada uno de los elementos puede formar parte de la agrupación, tantas veces como sea posible.
El número de variaciones con repetición de k elementos, que pueden formarse a partir de n elementos distintos ( Vkkn ) , es:

Permutación
En matemáticas, llamamos permutación a una variación del orden o de la disposición de los elementos de un conjunto.
Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
La definición intuitiva de p
|
Para ilustrar la definición, retomemos el ejemplo descrito en la introducción. En el ejemplo, X={1, 2, 3}.
Entonces, cada correspondencia uno a uno entre el conjunto {1, 2, 3} a sí mismo equivale a una forma de ordenar los elementos.
Por ejemplo, la asignación biyectiva dada por
- 1 → 1
- 2 → 2
- 3 → 3
puede hacerse corresponder al ordenamiento "1, 2, 3".
Por otro lado, la asignación biyectiva dada por
- 1 → 3
- 2 → 2
- 3 → 1
puede hacerse corresponder al ordenamiento "3, 2, 1".
En la definición de permutación, no se establece condición alguna sobre X, el cual puede incluso ser infinito. Sin embargo, es común considerar únicamente el caso en que X es un conjunto finito al estudiar permutaciones.
el tamaño, el orden, la repetición, la partición. Así un problema combinatorio consiste usualmente en establecer una regla sobre cómo deben ser las agrupaciones y determinar cuántas existen que cumplan dicha regla. Básicamente, dos asuntos: permutaciones y combinaciones (ambas sin repetición o con ella).
Un tipo importante de esas agrupaciones son las llamadas permutaciones. Dada una n-tupla ordenada de elementos de un conjunto, el número de permutaciones es el número de n-tuplas ordenadas .
Fórmula del número de permutaciones
Dado un conjunto finito  de
de 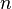 elementos, el número de todas permutaciones es igual a factorial de n:
elementos, el número de todas permutaciones es igual a factorial de n:
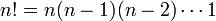 .
.
Demostración: Dado que hay 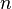 formas de escoger el primer elemento y, una vez escogido éste, sólo tenemos
formas de escoger el primer elemento y, una vez escogido éste, sólo tenemos 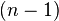 formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos
formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos ![[n-(k-1)] \,\!](https://upload.wikimedia.org/math/8/f/4/8f46046174b5f2caf438a978873d5f94.png) posibles elementos para escoger, lo que nos lleva a que tenemos
posibles elementos para escoger, lo que nos lleva a que tenemos 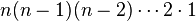 formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.  .
.
Ejemplo: sea el conjunto A={1,2,3} en este caso hay 6 permutaciones, en forma compacta: 123, 132, 213, 231, 312, 321. En álgebra, para estudiar los grupos simétricos se presentan entre paréntesis y en dos filas, en la primera siempre aparece 1 2 3.
Una variante de lo mismo, si se va a formar un comité que involucra presidente, tesorero y secretario, habiendo tres candidatos a, b, c ; cuando se elige por sorteo los cargos sucesivamente, hay seis posibilidades u ordenaciones: abc, acb, bca, bac, cab, cba. Heimer.
La primera forma de escribir una permutación σ, aunque no es la más compacta, consiste en escribirla en forma de matriz de dos filas, situando en la primera fila los elementos del dominio 1, 2, 3,...,n, y en la segunda las imágenes correspondientes a los elementos reordenados σ(1), σ(2), σ(3),...,σ(n).
Por ejemplo, dado el conjunto ordenado  podemos expresar una permutación
podemos expresar una permutación  sobre éste mediante una matriz de correspondencias:
sobre éste mediante una matriz de correspondencias:
Claramente es biyectiva, ya que podemos encontrar una aplicación inversa  de forma que su composición genera la aplicación identidad. Para ello, en primer lugar intercambiamos las filas y finalmente reordenamos las columnas de modo que los elementos del dominio queden ordenados de forma natural:
de forma que su composición genera la aplicación identidad. Para ello, en primer lugar intercambiamos las filas y finalmente reordenamos las columnas de modo que los elementos del dominio queden ordenados de forma natural:
Notación de ciclos
Existe otra notación más compacta, llamada notación de ciclos. Un ciclo de longitud s es una permutación que intercambia cíclicamente s elementos y fija los restantes.
Esta notación revela mejor la estructura interna de la permutación. Para ello:
- Empezamos con cualquier elemento. Lo escribimos, a su derecha escribimos su imagen, a la derecha de esta, la imagen de su imagen, y seguimos así hasta que se complete un ciclo.
- Luego cogemos cualquier elemento no contenido en el primer ciclo, volvemos a escribir su imagen a su derecha, y continuamos hasta completar el segundo ciclo.
- El proceso continúa hasta que la permutación entera ha quedado descrita como producto de ciclos disjuntos.
Siguiendo con el mismo ejemplo de antes, en notación de ciclos,  quedaría expresada como composición de dos ciclos:
quedaría expresada como composición de dos ciclos:
-
 = (1 3 5 6 )(2 4 7 8)
= (1 3 5 6 )(2 4 7 8)
Descomposición de una permutación en ciclos disjuntos
La descomposición realizada por el procedimiento anterior no es única en principio, pues podrían haberse obtenido cualquiera de estos resultados equivalentes:
-
 = (1 3 5 6)(2 4 7 8)=(2 4 7 8) (1 3 5 6)= (8 2 4 7)(6 1 3 5)
= (1 3 5 6)(2 4 7 8)=(2 4 7 8) (1 3 5 6)= (8 2 4 7)(6 1 3 5)
La descomposición canónica de una permutación como producto de ciclos se obtiene colocando en primer lugar de cada ciclo el número más pequeño del mismo. Posteriormente se procede a la colocación de los ciclos, colocando primero el ciclo cuyo primer elemento sea menor. Frecuentemente, suelen omitirse los ciclos de longitud 1. Así la permutación (1 3)(2)(4 5) se escribe simplemente como (1 3)(4 5).
Descomposición de una permutación en trasposiciones
Una trasposición es una permutación que intercambia dos elementos y fija los restantes. Dicho de otro modo, es un ciclo de longitud 2. Una propiedad interesante es que cualquier permutación se puede construir como una composición de transposiciones, aunque no de manera única. Dadas dos descomposiciones en transposiciones de una permutación se cumple que ambas usaran un número par o ambas usarán un número impar, eso permite definir de manera unívoca la signatura de una permutación.
Las trasposiciones permiten descomponer una permutación cualquiera de una forma diferente a la descomposición en ciclos. En particular, las trasposiciones que aparezcan no tendrán que ser disjuntas: Por ejemplo, el ciclo (1 2 3 4) = (1 2) (2 3) (3 4). Aquí el orden de aplicación es importante: en primer lugar (3 4) deja el 4 en su sitio definitivo y el 3 descolocado. Después (2 3) deja en su sitio definitivo el 3 y el 2 descolocado, que quedará recolocado definitivamente por (1 2).
Para ver que cualquier permutación descompone como producto de trasposiciones bastará ver que todo ciclo lo hace. De hecho, la descomposición del ciclo de nuestro ejemplo se generaliza a la fórmula:
No habrá unicidad en la descomposición, ni siquiera en el número de trasposiciones necesarias. Pero se demuestra que si  admite dos descomposiciones distintas con n y con m trasposiciones, entonces n y m tendrán la misma paridad (serán simultáneamente pares o impares). Dada una permutación cualquiera, se define el siguiente morfismo de grupos:
admite dos descomposiciones distintas con n y con m trasposiciones, entonces n y m tendrán la misma paridad (serán simultáneamente pares o impares). Dada una permutación cualquiera, se define el siguiente morfismo de grupos:
Donde 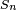 es el grupo simétrico de n elementos y m es un número entero, tal que exiten transposiciones
es el grupo simétrico de n elementos y m es un número entero, tal que exiten transposiciones  tales que:
tales que:
Permutación par y permutación impar
Llamaremos permutación par (resp. impar) a la que se escribe como composición de un número par (resp. impar) de trasposiciones.
Como ejemplo, de las 6=3! permutaciones del conjunto {1, 2, 3}, escritas en notación de ciclos:
- (1 2), (2 3) y (1 3) son, de forma trivial, impares.
- (1 2 3) y (1 3 2) son pares, como es fácil de comprobar al aplicar la fórmula anterior de descomposición de un ciclo en trasposiciones.
- e (la identidad) también es par.
En general, se demuestra que la mitad de las n! permutaciones de un conjunto de n elementos son pares y la otra mitad impares.
Combinaciones
También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):
- Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
- Sin repetición: como números de lotería (2,14,15,27,30,33)
1. Combinaciones con repetición
En realidad son las más difíciles de explicar, así que las dejamos para luego.
2. Combinaciones sin repetición
Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!
La manera más fácil de explicarlo es:
- imaginemos que el orden sí importa (permutaciones),
- después lo cambiamos para que el orden no importe.
Volviendo a las bolas de billar, digamos que queremos saber qué 3 bolas se eligieron, no el orden.
Ya sabemos que 3 de 16 dan 3360 permutaciones.
Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.
Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:
| El orden importa | El orden no importa |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 |
1 2 3 |
Así que las permutaciones son 6 veces más posibilidades.
De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:
3! = 3 × 2 × 1 = 6
(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)
Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):
![]()
Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:
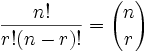 |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden no importa) |
Y se la llama "coeficiente binomial".
Notación
Además de los "grandes paréntesis", la gente también usa estas notaciones:

Ejemplo
Entonces, nuestro ejemplo de bolas de billar (ahora sin orden) es:
| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
O lo puedes hacer así:
| 16×15×14 | = | 3360 | = 560 |
| 3×2×1 | 6 |
Así que recuerda, haz las permutaciones, después reduce entre "r!"
... o mejor todavía...
¡Recuerda la fórmula!
Es interesante darse cuenta de que la fórmula es bonita y simétrica:

Con otras palabras, elegir 3 bolas de 16 da las mismas combinaciones que elegir 13 bolas de 16.
| 16! | = | 16! | = | 16! | = 560 |
| 3!(16-3)! | 13!(16-13)! | 3!×13! |
Principio de adición
Si un evento E puede ocurrir en m formas y un segundo evento F puede ocurrir en
n formas y ambos eventos no pueden ocurrir en forma simultánea entonces E o F
pueden ocurrir en m + n formas.
Ejemplos:
a) Existen 3 profesores y 2 profesoras que imparten la materia de cálculo. Un
estudiante puede escoger un profesor de 3 + 2 = 5 formas.
b) En una biblioteca hay 3 libros de novelas de misterio diferentes, 5 novelas de
romance y 4 novelas de aventura diferentes. Existen 3 + 5 + 4 = 12 formas de
escoger una novela.
c) Cinco empresas de transporte terrestre tienen servicio diario entre Mérida y
México. Tres empresas de aviación tienen vuelo diario entre Mérida y
México. En consecuencia, hay 5+3 maneras de ir de Mérida a México en
avión o en autobús. En los problemas de conteo, la palabra "o" se traduce en
suma.
d) Si tengo un billete de $50, uno de $100, uno de $200 y un billete de $1000,
¿Cuál es el número total de precios que puedo pagar usando algún o todos
mis billetes?
Este es un buen ejemplo de una situación en la que se necesita un listado
sistemático. Como tenemos 4 billetes de denominación diferente, debemos
considerar 4 casos. Éstos son, los precios que podemos cubrir con un billete, con 2
billetes, con 3 billetes y con 4 billetes. Se debe de examinar cada uno de estos casos
y luego aplicar el principio de adición.
• Con 1 billete podemos tener 4 precios: $50, $100, $200 y $1000.
• Con 2 billetes, podemos listar sistemáticamente las combinaciones:
i. Las que tienen $50 son: $50 + $100 = $150, $50+$200 =
$250, $50 + $1000 = $1050
ii. Las que tienen $100 y no hemos listado aún: $100 + $200 =
$300, $100+$1000 = 1100
iii. Y las que tienen $200 y tampoco hemos listado: $200 + $100
= $1200
• Con 3 billetes, las combinaciones son(una para cada billete que
falta):
i. $50 + $100 + $200 = $350 (falta la de $1000)
ii. $100 + $200 + $1000 = $1300 (falta la de $50)
iii. $50 + $200 + $1000 = $1250 (falta la de $100)
iv. $50 + $100 + $1000 = $1150 (falta la de $200)
• Con las cuatro billetes: $ 50 + $100 + $200 + $1000 = $1350
Principio de multiplicación
Si un evento puede efectuarse de n1 formas diferentes y si continuando el
procedimiento, un segundo evento puede realizarse de n2 formas diferentes y si
después de efectuados, un tercer elemento puede realizarse de n3 formas
diferentes, entonces el número de formas en que los eventos puede realizarse será
n1 × n2 × n3maneras diferentes
Ejemplos:
1. El menú de un restaurante ofrece 3 platos calientes y 4 postres. ¿De cuántas
maneras se puede elegir un almuerzo de 1 plato caliente y 1 postre?
Se puede hacer una lista de todas las posibilidades, pero es mucho más cómodo
aplicar el principio de la multiplicación:
Hay 3 maneras de elegir el plato caliente y para cada una de ellas hay 4 maneras de
elegir el postre. Por lo tanto, hay 3⋅ 4 =12 comidas posibles.
Ngj/v2008
2. ¿Cuántos códigos de una letra y un número de un dígito se pueden formar con
las 26 letras del alfabeto y los números 0, 1, 2,...,9?
Listando todas las posibilidades:
A0 A1 .... A9
B0 B1 .... B9
M M
Z0 Z1 .... Z9
hasta obtener 26 filas de 10 códigos en cada una: 26 ⋅10 = 260.
Es más simple utilizar el principio de multiplicación: hay 26 maneras de elegir la
letra y para cada una de ellas hay 10 maneras de elegir el número, de modo que son
26 ⋅10 = 260 códigos.
Nota que en los 2 ejemplos hay total libertad de elegir el segundo elemento,
no importa cómo se eligió el primero. Es decir, el segundo elemento es
independiente del primero. Elegido el plato caliente, podemos elegir cualquiera de
los 4 postres. Elegida la letra podemos agregarle cualquiera de los 10 números. Este
principio es útil cuando se puede descomponer el proceso de recuento en pasos
independientes.
Del problema de los 10 comensales, posiblemente parece increíble que 10
personas puedan colocarse en un número tan elevado de posiciones diferentes.
Comprobemos el cálculo. Ante todo, hay que aprender a determinar el número de
combinaciones distintas, posibles. Para mayor sencillez empecemos calculando un
número pequeño de objetos, por ejemplo, tres. Llamémosles A, B y C.
Deseamos saber de cuántos modos diferentes pueden disponerse,
cambiando mutuamente su posición. Hagamos el siguiente razonamiento. Si se
separa de momento el objeto C, los dos restantes, A y B, pueden colocarse
solamente en dos formas.
Ahora agreguemos el objeto C a cada una de las parejas obtenidas. Podemos
realizar esta operación tres veces:
• Colocar C detrás de la pareja,
• Colocar C delante de la pareja,
• Colocar C entre los dos objetos de la pareja.
Es evidente que no son posibles otras posiciones distintas para el objeto C, a
excepción de las tres mencionadas. Como tenemos dos parejas, AB y BA, el número
total de formas posibles de colocación de los tres objetos será: 2×3 = 6
Ahora hagamos el cálculo para 4 objetos, llamémosles A, B, C y D, y
separemos de momento uno de ellos, por ejemplo, el objeto D. Efectuemos con los
otros tres todos los cambios posibles de posición. Ya sabemos que para tres, el
número de cambios posibles es 6. ¿En cuántas formas diferentes podemos disponer
el cuarto objeto en cada una de las 6 posiciones que resultan con tres objetos?
Evidentemente, serán cuatro. Podemos:
• Colocar D detrás del trío,
• Colocar D delante del trío,
• Colocar D entre el 1º y de 2º objetos,
• Colocar D entre el 2º y 3º.
Obtenemos en total: 6× 4 = 24 posiciones, pero teniendo en cuenta que
6 = 2× 3 y que 2 = 1× 2 , entonces podemos calcular el número de cambios posibles
de posición haciendo la siguiente multiplicación: 1× 2× 3× 4 = 24
Razonando de manera idéntica, cuando haya 5 objetos, hallaremos que el
número de formas distintas de colocación será igual a: 1× 2× 3× 4× 5 = 120
Para 6 objetos será: 1× 2× 3× 4× 5× 6 = 720 y así sucesivamente.
Volvamos de nuevo al caso antes citado de los 10 comensales. Sabremos el
número de posiciones que pueden adoptar las 10 personas alrededor de la mesa, si
nos tomamos el trabajo de calcular el producto siguiente:
1× 2× 3× 4× 5× 6× 7 ×8× 9×10 . El resultado es 3’628,800.
El cálculo sería más complicado, si de los 10 comensales, 5 fueran
muchachas y desearan sentarse a la mesa alternando con los muchachos. A pesar
de que el número posible de combinaciones se reduciría en este caso
considerablemente, el cálculo sería más complejo.
Supongamos que se sienta a la mesa, indiferentemente del sitio que elija,
uno de los jóvenes. Los otros cuatro pueden sentarse, dejando vacías para las
muchachas las sillas intermedias, adoptando 1× 2×3× 4 = 24 formas diferentes.
Como en total hay 10 sillas, el primer joven puede ocupar 10 sitios distintos. Esto
significa que el número total de combinaciones posibles para los muchachos es de
10× 24 = 240 .
¿En cuántas formas diferentes pueden sentarse en las sillas vacías, situadas
entre los jóvenes las 5 muchachas? 1× 2× 3× 4× 5 = 120
Combinando cada una de las 240 posiciones de los muchachos, con cada una
de las 120 que pueden adoptar las muchachas, obtendremos el número total de
combinaciones posibles, o sea 240×120 = 28,800 .
Este número, como vemos, es muchas veces inferior al que hemos citado
antes y se necesitaría un total de 79 años. Los jóvenes clientes del restaurante, que
vivieran hasta la edad de cien años, podrían asistir a una comida, servida gratis,
sino por el propio camarero, al menos por uno de sus descendientes.
Binomio de Newton
En matemática, el teorema del binomio es una fórmula que proporciona el desarrollo de la potencia n-ésima de n (siendo n, entero positivo) de un binomio. De acuerdo con el teorema, es posible expandir la potencia (x + y)n en una suma que implica términos de la forma axbyc, donde los exponentes b y c son números naturales con b + c = n, y el coeficiente a de cada término es un número entero positivo que depende de n y b. Cuando un exponente es cero, la correspondiente potencia es usualmente omitida del término. Por ejemplo,
El coeficiente a en el término de xbyc es conocido como el coeficiente binomial 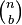 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).
Este teorema establece: Usando la fórmula para calcular el valor de 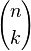 (que también es representado ocasionalmente como
(que también es representado ocasionalmente como  o
o 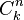 ) se obtiene la siguiente representación:
) se obtiene la siguiente representación:
|
|
|
donde 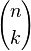 recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:
recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:
|
|
Ejemplo
Como ejemplo, para n=2, n=3, n=4, utilizando los coeficientes del triángulo de pascal:
(2)
Para obtener la expansión de las potencias de una resta, basta con tomar -y en lugar de y en el caso anterior. La expresión (2) queda de la siguiente forma:
Teorema generalizado del binomio (Newton)
Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita:
(3)
Donde r puede ser cualquier número real (en particular, r puede ser cualquier número real, no necesariamente positivo ni entero), y los coeficientes están dados por:
(el k = 0 es un producto vacío y por lo tanto, igual a 1; en el caso de k = 1 es igual a r, ya que los otros factores (r − 1), etc., no aparecen en ese caso).
Una forma útil pero no obvia para la potencia recíproca:
La suma en () converge y la igualdad es verdadera siempre que los números reales o complejos x e y sean suficientemente cercanos, en el sentido de que el valor absoluto | x/y | sea menor a uno.
Coeficiente binomial
Para aplicar el Teorema del binomio, el coeficiente binomial se presenta como  de forma sencilla:
de forma sencilla:
Historia
Atribuido a Newton, el teorema fue en realidad descubierto por primera vez por Abu Bekr ibn Muhammad ibn al-Husayn al-Karaji alrededor del año 1000. Aplicando los métodos de John Wallis de interpolación y extrapolación a nuevos problemas, Newton utilizó los conceptos de exponentes generalizados mediante los cuales una expresión polinómica se transformaba en una serie infinita. Así estuvo en condiciones de demostrar que un gran número de series ya existentes eran casos particulares, ya fuera diferenciación o bien por integración.
El descubrimiento de la serie binómica es un resultado importante de por sí; sin embargo, a partir de este descubrimiento Newton tuvo la intuición de que se podía operar con series infinitas del mismo modo que con expresiones polinómicas finitas.
Newton no publicó nunca el teorema del binomio. Lo hizo Wallis por primera vez en 1685 en su Álgebra, atribuyendo a Newton este descubrimiento.
El teorema binómico para n=2 se encuentra en los Elementos de Euclides (300 a. C.), asimismo el término «coeficiente binomial» fue introducido por Michel Stifer en el siglo XVI.
Los binomios se resuelven también con expresiones algebraicas.
Triangulo de Pascal
En matemática, el triángulo de Pascal es una representación de los coeficientes binomiales ordenados en forma triangular. Es llamado así en honor al matemático francés Blaise Pascal, quien introdujo esta notación en 1654, en su Traité du triangle arithmétique. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta.
La construcción del triángulo está relacionada con los coeficientes binomiales según la fórmula (también llamada Regla de Pascal). Si  entonces
entonces  para todo entero positivo n y todo entero positivo k entre 0 y n.
para todo entero positivo n y todo entero positivo k entre 0 y n.
El triángulo de Pascal se puede generalizar a dimensiones mayores. La versión de tres dimensiones se llama pirámide de Pascal o tetraedro de Pascal, mientras que las versiones más generales son llamadas simplex de Pascal.

La primera representación explícita de un triángulo de coeficientes binomiales data del siglo X, en los comentarios de los Chandas Shastra, un libro antiguo indio de prosodia del sánscrito escrito por Pingala alrededor del año 200 a.C.
Las propiedades del triángulo fueron discutidas por los matemáticos persas Al-Karaji (953–1029) y Omar Khayyám (1048–1131); de aquí que en Irán sea conocido como el triángulo Khayyam-Pascal o simplemente el triángulo Khayyam. Se conocían también muchos teoremas relacionados, incluyendo el teorema del binomio.
En China, este triángulo era conocido desde el siglo XI por el matemático chino Jia Xian (1010–1070). En el siglo XIII, Yang Hui (1238–1298) presenta el triángulo aritmético, equivalente al triángulo de Pascal, de aquí que en China se le llame triángulo de Yang Hui.
Petrus Apianus (1495–1552) publicó el triángulo en el frontispicio de su libro sobre cálculos comerciales Rechnung (1527). Este es el primer registro del triángulo en Europa. En Italia, se le conoce como el triángulo de Tartaglia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77). También fue estudiado por Michael Stifel (1486 - 1567) y François Viète (1540-1603).
En el Traité du triangle arithmétique (Tratado del triángulo aritmético) publicado en 1654, Blaise Pascal reúne varios resultados ya conocidos sobre el triángulo, y los emplea para resolver problemas ligados a la teoría de la probabilidad; demuestra 19 de sus propiedades, deducidas en parte de la definición combinatoria de los coeficientes. Algunas de estas propiedades eran ya conocidas y admitidas, pero sin demostración. Para demostrarlas, Pascal pone en práctica una versión acabada de inducción matemática. Demuestra la relación entre el triángulo y la fórmula del binomio. Fue bautizado Triángulo de Pascal por Pierre Raymond de Montmort (1708) quien lo llamó: Tabla del Sr. Pascal para las combinaciones, y por Abraham de Moivre (1730) quien lo llamó: "Triangulum Arithmeticum PASCALIANUM" (del latín: "Triángulo aritmético de Pascal"), que se convirtió en el nombre occidental moderno.
l triángulo de Pascal se construye de la siguiente manera: se comienza en el número «1» centrado en la parte superior; después se escriben una serie de números en las casillas situadas en sentido diagonal descendente, a ambos lados, del siguiente modo: se suman las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) se escribe debajo de dichas casillas; el proceso continúa escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3), etc. De manera general, esto se cumple así debido a la regla de Pascal, que indica que  para todo entero positivo n y todo entero positivo k entre 0 y n. En la ilustración, en la última fila, la cifra 4 cuyas casillas situadas sobre ella corresponden a las cifras 1 y 3, se cumple que
para todo entero positivo n y todo entero positivo k entre 0 y n. En la ilustración, en la última fila, la cifra 4 cuyas casillas situadas sobre ella corresponden a las cifras 1 y 3, se cumple que  , para la cifra 6 se cumple
, para la cifra 6 se cumple  y para la última cifra 4
y para la última cifra 4  ; de igual manera, se cumple propiedad para las demás filas.
; de igual manera, se cumple propiedad para las demás filas.

Por lo tanto, todas los cifras escritas en cada fila del triángulo, corresponden a los coeficientes del desarrollo binomial de la potencia de una suma
Vínculo entre el triángulo de Pascal y el binomio de Newton
La expresión que proporciona las potencias de una suma 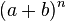 se denomina binomio de Newton.
se denomina binomio de Newton.
En esta expresión, lo único que se desconoce son los coeficientes de los monomios, de manera que la relación con el triángulo de Pascal es la siguiente:
|
Se puede generalizar este resultado para cualquier valor de n ∈ N por inducción matemática.
Propiedades del triángulo de Pascal

 . Los casillas exteriores, (en azul) tienen valor nulo y las casillas en violeta proporcionan un ejemplo de la regla de Pascal.
. Los casillas exteriores, (en azul) tienen valor nulo y las casillas en violeta proporcionan un ejemplo de la regla de Pascal.Cada uno de los valores de un triángulo de Pascal escritos en forma de tabla corresponden a un coeficiente de la expansión de una potencia de sumas. Concretamente, el número en la línea n y la columna p corresponde a  , o también denotado como
, o también denotado como  (
( por "combinación") y se dice «n sobre p», «combinación de n en p» o «coeficiente binomial n, p». Las casillas vacías corresponden a valores nulos. Usando las propiedades de los coeficientes binomiales, se pueden obtener las siguientes propiedades de cualquier triángulo de Pascal con todo rigor:
por "combinación") y se dice «n sobre p», «combinación de n en p» o «coeficiente binomial n, p». Las casillas vacías corresponden a valores nulos. Usando las propiedades de los coeficientes binomiales, se pueden obtener las siguientes propiedades de cualquier triángulo de Pascal con todo rigor:
- Los valores de cada fila del triángulo guardan simetría respecto al eje vertical imaginario del mismo, debido a que
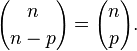
- Los valores correspondientes a la zona fuera del triángulo tienen valor 0, puesto que
 cuando p > n.
cuando p > n.
- Y claro, la regla de Pascal de construcción del triángulo da la relación fundamental de los coeficientes binomiales

Una consecuencia interesante del triángulo de Pascal es que la suma de todos los valores de una fila cualquiera del triángulo es una potencia de 2. Esto es debido a que, por el teorema del binomio, la expansión de la n-potencia de (1 + 1)n = 2n es
que corresponde precisamente con la suma de todos los valores de la n-ésima fila de un triángulo de Pascal.
Otras representaciones del triángulo
La ilustración al comienzo del artículo muestra el triángulo de Pascal dibujado como un triángulo equilátero. Es posible «enderezarlo» de tal forma que su dibujo quede como un triángulo rectángulo. De esta forma, a la izquierda queda una columna de números «1». La siguiente columna deja un lugar vacío en la primera fila y sigue con la sucesión de números naturales: 1, 2, 3, 4, ..., n, .... La tercera columna deja dos filas vacías y comienza con la sucesión de los números triangulares: 1, 3, 6, 10, 15, .... Dibujado de esta manera es fácil ver que:
- Cada número en una columna cualquiera es igual a la suma parcial de los elementos de la columna anterior (a la izquierda) hasta la fila anterior en orden descendente.
- La tercera columna es la sucesión de los números triangulares; la cuarta, la de los números tetraédricos; la quinta, la de los números pentaédricos, y así sucesivamente.
Generalizaciones
En vez de considerar las potencias de a + b, se puede considerar las del trinomio a + b + c. De esta manera, (a + b + c)n es una suma de monomios de la forma λp, q, r ·ap·bq·cr, con p, q y r positivos, p + q + r = n, y λp, q, r un número natural que se llama coeficiente trinomial. Los cálculos son similares a los del coeficiente binomial, y se dan mediante la siguiente expresión:
-
 ,
,
en subconjuntos de p, q y r elementos.
Estos coeficientes se pueden considerar como la analogía tridimensional del triángulo de Pascal. De hecho, a la distribución de estos coeficientes al estilo piramidad se le conoce como pirámide de Pascal; es también infinita, con secciones triangulares, y el valor en cada casilla es la suma de los valores de las tres casillas encima de ella.
En esta pirámide se observa una invariante por rotación de 120 grados alrededor de un eje vertical que pasa por el vértice. El triángulo de Pascal aparece en las tres caras de la pirámide.
De igual manera, todo esto se puede generalizar a dimensiones finitas cualquieras, pero sin la posibilidad de hacer dibujos explicativos sencillos.

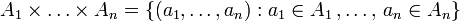
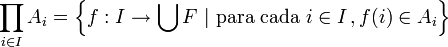
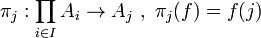
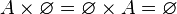
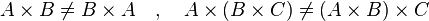
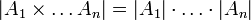

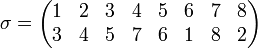


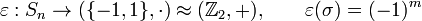
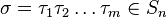


 en el desarrollo de
en el desarrollo de 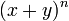 es
es